Submitted by Dr Ulrich Schneider on Mon, 18/04/2016 - 12:26
Our paper on the dimensional crossover of Many-body localization was published as an Editor's suggestion in PRL.
In this work we could show that individual localized systems can-when coupled together-start to act as a bath for themselves and restore ergodic behavior.
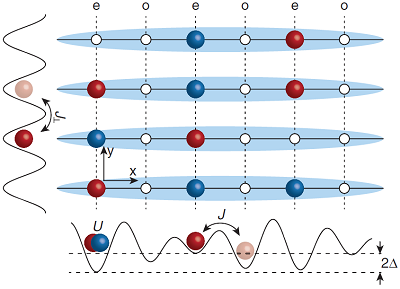
Many-Body Localization (MBL) represents a generic alternative to thermalization in isolated quantum systems, it describes interacting systems that cannot act as a bath for themselves and can therefore not be describes by standard statistical physics. Using a gas of ultracold fermions in an optical lattice, we artifically prepare an initial charge density wave in an array of 1D tubes with quasi-random onsite disorder and monitor the subsequent dynamics over several thousand tunneling times. We find a strikingly different behavior between MBL and Anderson Localization. While the non-interacting Anderson case remains localized, in the interacting case any coupling between the tubes leads to a delocalization of the entire system.
Phys. Rev. Lett. 116, 140401 (2016)
